my research
Lagrangian Mean Curvature Flow
Given a geometric object (such as a curve, surface, or manifold), one may ask: what is the optimal representation of this object?, where the meaning of "optimal" depends on the person asking the question. Geometric evolution equations are one approach to optimization, inspired by the way heat dissipates to a steady-state temperature distribution. The hope is that the "optimal" shape will be optimal not only quantitatively (e.g., shortest) but also qualitatively (e.g., most symmetric).
My primary interest in this area is mean curvature flow, which arises when we consider submanifolds and take "optimal" to mean "smallest local area". I am also interested in other flow techniques, such as the Ricci flow and Hermitian curvature flow, which study Riemannian and Hermitian metrics and for which "optimal" means "solves Einstein's equations".
Unlike the ordinary heat equation, none of these flows is a linear PDE, we expect to encounter singularities before reaching minimizers; these singularities need to be resolved in some coherent scheme in order to continue the flow and proceed toward the optimizer. In order to do this, one must have a very clear picture of what exactly happens to cause the flow to become singular. One also hopes to be able to describe the gross structure of the object in terms of where and how the singularities develop.
The case of Lagrangian submanifolds of a Calabi-Yau manifold (of which a curve in the plane is the simplest example) is the focus of my research. I am also interested in applying these ideas to Legendrian submanifolds of a contact manifold.
- Polygon Curvature Flow (with my Summer 2014 REU group: Jessie de la Cruz Santos, Ryan Gallagher, and Sarah Hadaidi)
Is there a Grayson's Theorem for polygons? - Singularities of the Lagrangian Mean Curvature Flow, submitted
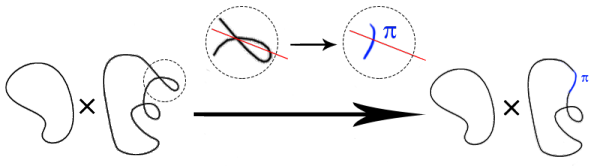
Well-behaved singularities of Lagrangian mean curvature flow occur only at certain times, which can be read off from the first cohomology of the initial data. Ill-behaved singularities are not too ill-behaved: they are modeled by special Lagrangian cones. - A Maximum Principle for Circle-Valued Temperatures, to appear in Advances in Geometry
Some thermometers are linear (like a bulb thermometer); others have a dial. What if your dial thermometer spun all the way around? This paper adapts a classical result about how heat flows--out of hot spots and into cold spots--to a statement you can use even if you only have a blown-out dial thermometer. - A Characterization of the Singular Time of the Mean Curvature Flow, 2011, Proceedings of the AMS
This paper answers the question: what happens to cause a mean curvature flow to become singular? - Mean Curvature Flow in Higher Codimension, 2011, Ph.D. Thesis, Michigan State University.
Smooth singularity modeling for the mean curvature flow and singularities of Lagrangian mean curvature flow.
Chromatic Homology and Its Generalizations
The chromatic polynomial is a classical invariant (introduced by Birkhoff in 1912) of graphs which measures colorability. This polynomial invariant was categorified to a homology theory by Helme-Guizon and Rong in 2004, and (in a somewhat different way) by Eastwood and Huggett in 2007. Radmila Sazdanovic and I have generalized both the Helme-Guizon-Rong construction and the Eastwood-Huggett construction (with Vin de Silva) to give homology theories which are invariants of simplicial complexes. In particular, this homology theory yields a new polynomial invariant of simplicial complexes, whose interpretation remains somewhat mysterious.
I am also interested in how we could view any or all the flavors of chromatic homology (Eastwood-Huggett's, Helme-Guizon-Rong's, or Sazdanovic's and my version) as counting solutions of some elliptic PDE.
- On Configuration Spaces and Simplicial Complexes (with Vin de Silva and Radmila Sazdanovic), submitted
- State Sum Homology for Simplicial Complexes (with Radmila Sazdanovic)